THE PHYSICS OF FORCE

ARE YOU SURE YOU KNOW WHAT FORCE IS? Force as a word is not strange to many, but the scope and concept of force is largely unknown by many. While this may because a few consider this knowledge unimportant to their field, others haven't just been opportuned to learn about it. The idea of this write-up is to bridge the gap between being oblivious on the subject and possessing a basic knowledge of it. Learning new things could be fun, especially about concepts of natural quantities that constitute the world we live in.

PRODUCTION OF FORCE

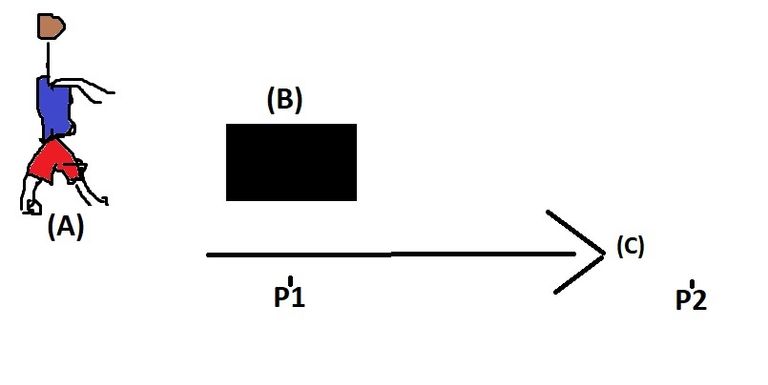
Let's consider the above scenario; a person(A) attempts pushing a box(B) from a point(P1) to another point(P2) along a path(C). If no disturbance or external influence acts on this box(B), this box we remain in its position without moving (this is inertia).

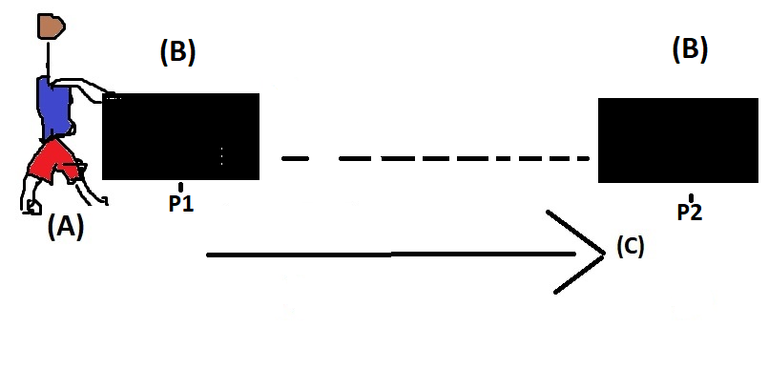
In the case, the person(A) pushes this box(B) from P1 to P2 along path C. It is obvious that an agent exerted by the person(A) acted on the box that made it change its position from P1 to P2. Although an abstract agent, its effect is obvious. That agent which acted on the box(B) and made it change its position from P1 to P2, is the FORCE. We can observe that the force came from a source. We therefore say that all force a produced by a source. The source- which could vary in different instances- in this case is the person(A). Mind you, exertion of forces are not only isolated to cases like this; where a push occurs. Pulling a body would as well exert force on that body and can make it change its position as well.

NEWTONIAN FORCE
Sir Isaac Newton in 1687 explained motion of a body using inertia and force. He proposed three laws of motion that have had monumental impacts in physics. In his second law of motion he simply stated that; Acceleration of a body is directly proportional to the net force acting on the body, where the mass of that body is constant.

MATHEMATICAL REPRESENTATION OF FORCE
From the law;

F < a (we use '<' sign to denote 'directly proportional) . . . . . . . . . . . . . . (eqn 1)

this equation becomes;
Force(F) = mass(m) x acceleration(a) . . . . . . . . . . .(eqn 2)

=> F = m x a . . . . . . . . . . . . . . . . . . . . . . .(eqn 3)

where m = mass and is the constant of proportionality.

DEFINITION OF FORCE
From the equation(2) above, we therefore define force as the product of mass and acceleration of a body. It is an influence that causes the change in position and velocity of a body. The unit of force is Newton (named after Isaac Newton). The rotational version of force is TORQUE.

VARIATIONS OF THE FORCE EQUATION
The newtonian force equation F = ma, which could be called the basic force equation, has variations that is dependent on the kind of force. Regardless of the variation it still mirrors the basic force equation. Let's look at an example:

Consider the quantity; weight of a body. Weight is a force. weight is earth's gravitational pull on a body. Against what a few may have believed before now, weight is not mass. They are two different quantities. While weight of a particular body may vary in two different locations on the earth's surface, mass does not. Mass is more like the measure of matter constituents of a body, while weight, like I said, is a force.

Mathematically, weight is written as;
Weight = m x g . . . . . . . . . . . . . . . . . . . . . . . .(eqn4)

where; m = mass of the body
       g = acceleration due to gravity 

If you compare this equation (eqn3) of weight with our basic force equation as in equation(1) above, you can see that they are both the same.

Force = m x a
Weight = m x g

The 'a' and 'g' both represent accelerations. Only difference there is the fact that 'g' is specified as acceleration due to gravitational
force.

EFFECTS OF FORCE

MOTION: Motion is the change of position of a body. A body is caused to change position when a force which is higher than and opposes the force that keeps the body at rest is exerted on the body. From our first example, for the box to change position from P1 to P2, the force exerted by the person(A) on that box(b) has to be higher that the force of gravity holding that body at rest.

CHANGE IN VELOCITY (ACCELERATION):
Consider a body moving at a constant velocity, it will continue to move in that velocity unless influenced by an external force. This force causes it to change velocity. This change in velocity could be acceleration (where the velocity is increased) or deceleration (where the velocity is reduced)

TYPES OF FORCES
Not to go to the complexities of force, we will state some types of force in classical mechanics only. They are:

1. Gravitational force
2. electromagnetic force
3. Normal force
4. Frictional force
5. Centripetal force
6. Tension