নিউটনীয় বলবিদ্যা দুটো বস্তুপিণ্ডের পারস্পরিক মাধ্যাকর্ষণের প্রভাবজনিত পরিস্থিতির ব্যাখ্যা করে কিন্তু বস্তুপিণ্ডের সংখ্যা দুইয়ের বেশি হলেই গাণিতিক জটিলতা বৃদ্ধি পায়। সেইজন্য ফরাসী গণিতবিদ জোসেফ লুই লাগ্রাঞ্জ (১৭৩৬ খৃষ্টাব্দ – ১৮১৩ খৃষ্টাব্দ) কোনও একটি তন্ত্রে যাদৃচ্ছিক সংখ্যক (arbitrary number) বস্তুপিণ্ডের মধ্যেকার মাধ্যাকর্ষণজনিত পারস্পরিক ক্রিয়াকে সহজে বোঝার অভিপ্রায়ে গাণিতিক পদ্ধতিকে কাজে লাগিয়েছিলেন।
তিনি বস্তুপিণ্ডগুলির ভ্রমণপথের প্রতিটি বিন্দুতেই প্রতিটি বস্তুপিণ্ডের উপর প্রতিটি বস্তুপিণ্ডের মাধ্যাকর্ষণজনিত পারস্পরিক ক্রিয়াকে এক সহজ সরল পন্থায় নির্ণয় করতে গণিত প্রয়োগ করেন। যে ভ্রমণপথে যাত্রাকালের পরিসরে চলমান বস্তুর উপর ক্রিয়া সর্বনিম্ন হয়। এই পন্থায় বস্তুপিণ্ডের গতীয় শক্তি (kinetic energy) ও স্থৈতিক শক্তির (potential energy) ব্যবধান নির্ণয় করে বস্তুপিণ্ডের গতিপথ নির্ধারিত হয়।
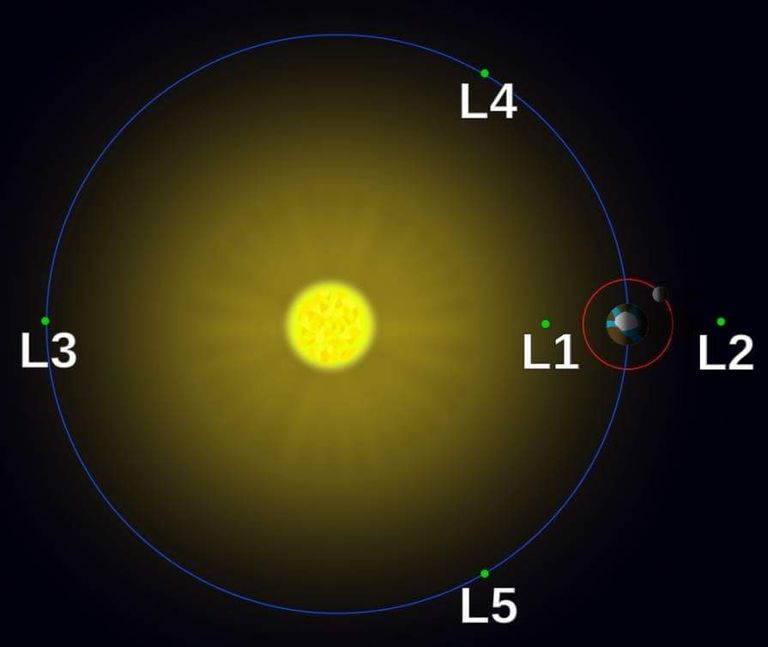
চিরায়ত গাগনিক বলবিদ্যায় (classical celestial mechanics) লাগ্রাঞ্জের গাণিতিক পদ্ধতি প্রয়োগ করে উভয়ের যৌথ ভরকেন্দ্রের চারপাশে প্রদক্ষিণরত একটি বিশাল ও একটি মাঝারি ভরবিশিষ্ট বস্তুপিণ্ডের মাধ্যাকর্ষণ ক্ষেত্রে আরও একটি অত্যন্ত ক্ষুদ্র এবং উপেক্ষণীয় ভরবিশিষ্ট বস্তুপিণ্ডের গতিপথ ও অবস্থানের সুস্থিতি সম্বন্ধে এক নতুন ধারণা পাওয়া গিয়েছিল। এক্ষেত্রে লাগ্রাঞ্জীয় বিন্দু ল-৪ (L-4) এবং ল-৫ (L-5) –এর অবস্থানে উপেক্ষণীয় ভরবিশিষ্ট বস্তুটির সুস্থির অবস্থানের জন্য বিশাল বস্তুপিণ্ডটির (ধরা যাক সূর্য) ভর মাঝারি বস্তুপিণ্ডটির (ধরা যাক পৃথিবী) ভরের চেয়ে ২৪.৯৬ গুণ বেশি হতেই হবে। এই শর্ত লঙ্ঘিত হলে উপেক্ষণীয় ভরবিশিষ্ট বস্তুটি ল-৪ এবং ল-৫–এর অবস্থানে সুস্থির থাকবে না।
লাগ্রাঞ্জের গণনায় দেখা যায় – বৃহৎ দুটো বস্তুপিণ্ডের অবস্থান সাপেক্ষ ল-১ (L-1), ল-২ (L-2), ল-৩ (L-3), ল-৪ (L-4) এবং ল-৫ (L-5) বিন্দুগুলোতে উপেক্ষণীয় ভরবিশিষ্ট বস্তুপিণ্ডটি মহাশূন্যে ভ্রমণরত বিশাল ও মাঝারি ভরবিশিষ্ট বস্তুপিণ্ডের অবস্থান সাপেক্ষ স্থির থাকে। এই পাঁচটি বিন্দুকেই গণিতবিদ লাগ্রাঞ্জের সম্মানে ‘লাগ্রাঞ্জীয় বিন্দু’ নামে চিহ্নিত করা হয়েছে (চিত্র-১.১)। এই পাঁচটি বিন্দুর মধ্যে কেবলমাত্র ল-৪ এবং ল-৫ বিন্দুতেই উপেক্ষণীয় ভরবিশিষ্ট বস্তুপিণ্ডটি বড় দুটি বস্তুপিণ্ডের অবস্থান সাপেক্ষ অত্যন্ত সুস্থির থাকে, কিন্তু ল-১, ল-২ এবং ল-৩ -- এই তিনটি বিন্দুতে উপেক্ষণীয় ভরবিশিষ্ট বস্তুপিণ্ডটি অপেক্ষাকৃত কম সুস্থির।
বিষয়টিকে আরও সহজ ও সরলভাবে ব্যাখ্যা করতে একটা উদাহরণের সাহায্য নিয়ে ধরা যাক – পাহাড়ের একেবারে চূড়ায় একটা ফুটবল স্থিরভাবে রাখা আছে। বাতাসের প্রবল বেগের কারণে ফুটবলটা সহজেই স্থিরাবস্থা থেকে গতিশীল হয়ে পাহাড়ের একেবারে চূড়া থেকে পাদদেশে নেমে আসতে পারলেও আর সহজে পাহাড়ের চূড়ায় পৌঁছাতে পারবে না। অর্থাৎ সামান্য বাহ্যিক বলের প্রভাব স্থিতিশীলতা নষ্ট করে দেওয়ার জন্য যথেষ্ট। উদাহরণটা ল-১, ল-২ এবং ল-৩ --এই তিনটি বিন্দুর সুস্থিরতার সঙ্গে তুলনীয়। অপরদিকে ফুটবলটাকে একটা মাঠের সবচেয়ে নীচু জায়গায় রাখলে যেমন হয় ঠিক সেই রকম ল-৪ এবং ল-৫ বিন্দুর সুস্থিতি। বাতাসের প্রবাহ এক্ষেত্রে ফুটবলটার অবস্থান পরিবর্তন করার সামান্য চেষ্টা করলেও কিছুক্ষণ পর ফুটবলটা মাধ্যাকর্ষণের প্রভাবে পুনরায় আগের অবস্থানে ফিরে আসবে। অর্থাৎ সামান্য বাহ্যিক বলের প্রভাব স্থিতিশীলতা নষ্ট করতে চেষ্টা করলেও পুনরায় স্থিতিশীল অবস্থানে ফিরে আসবে।