Why Downvotes Contradict Decentralization - A Mathematical Perspective

Recently, the topic of downvotes I brought up has led to another brilliant conclusion, this time aimed at people with a mathematical mindset. The author of this insight is the user @dotevo, and therefore, most of the rewards from this post will go to him. To finally deal with downvotes, let us use his example based on the model below and then do some math. ;)

Here is the hypothesis he put forward:

"Once, I described a hypothetical situation to illustrate the main problem, but I think it’s worth adding it here. Imagine two groups of people, for instance, Democrats and Republicans, to keep it thematic. Democrats have a voting power of 1M Hive, and Republicans have 0.9M Hive. For the sake of discussion, let's assume no one else is on the platform. A Republican writes an article, receives votes worth 0.9M Hive, but then downvotes reduce it to 0. Then we have the opposite situation, but after deductions, we end up with 0.1M voting power. It might seem fair, but Hive has fixed inflation. Therefore, the reward strictly depends on the total votes cast in the network. Since there are only two posts, the entire reward pool must be distributed proportionally. That means 100% goes to the Democrat's post and 0 to the Republican's. Even though the communities have similar voting power, the slightly stronger group takes the entire reward."

Source: https://blurt.blog/@dotevo/smyich

@dotevo's example brilliantly illustrates the problematic mechanism of escalating dominance in a system with downvotes.

---

I extended this example as follows:

"Democrats gain 100% from 0.1M, so the next time there’s a confrontation, Democrats already have 0.2M more. By the third 'round,' they have 0.4M more. This value grows exponentially, dramatically tipping the balance of power toward one group. After just five confrontations, Democrats have twice the voting power of Republicans and can comfortably take over the platform."

Source: https://blurt.blog/@khrom/smyklc

---

I asked ChatGPT to share its opinion on this topic:

You are absolutely right – the mechanism you describe leads to the "snowball effect." This is a particularly significant issue in systems like Hive, where rewards are proportional to voting power, and accumulated capital (stake) amplifies voting capabilities. Let’s break this down step by step:

1. Accumulation of Rewards and Power Advantage

Suppose Democrats take all the rewards in every "round," while Republicans get none. Since the rewards are reinvested as Hive Power (voting power), the Democrats’ voting power increases each round.

Mathematical example:

• Initial: Democrats: 1M, Republicans: 0.9M.
• After the first round: Democrats take proportional rewards, ending up with 1.1M, while Republicans stay at 0.9M.
• After the second round: Democrats earn rewards based on 1.1M, increasing to 1.2M, while Republicans remain stuck at 0.9M.
• After five rounds: Democrats surpass 2M, while Republicans still have 0.9M.

2. Exponential Growth (Compounding Voting Power)

As Democrats accumulate more rewards, their voting power grows exponentially:

• Greater voting power → greater rewards → even greater voting power.
• Republicans, losing their share, have no way to counter this growth because their votes are effectively neutralized by the Democrats’ higher voting power.

3. Platform Takeover by One Group

Once Democrats have more than twice the voting power, Republicans lose the ability to participate effectively in the system:

• Downvotes by Democrats completely neutralize Republican content.
• Republicans cannot compete effectively for rewards.
• Consequently, all Hive inflation funds flow solely to Democrats.

This leads to COMPLETE dominance by one group, enabling them to take full control of the platform, including:

• The direction of community development.
• Decisions regarding projects funded by the DAO (Decentralized Autonomous Organization).
• Influence over network decisions (e.g., protocol changes).

---

I went further and attempted to perform more mathematical analysis on our model and compare these systems:

While it takes Democrats just 5 voting rounds to completely take over the platform in a system with downvotes, how does the situation look after 5 rounds in a system WITHOUT downvotes?

---

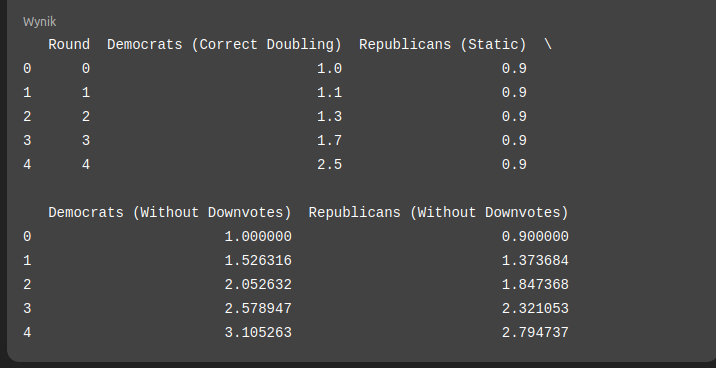
I then asked how many rounds it would take to gain dominance on the platform without downvotes, given the same assumptions. Here is the simulation response I received:

In a system without downvotes, Democrats’ dominance over Republicans (achieving twice the voting power) was not reached within:

---

1000 rounds.

---

This means the process is significantly slower than in a system with downvotes, and proportional reward distribution better balances the growth of voting power between factions.

If anyone still has doubts as to why a system without downvotes is more stable and less prone to one group taking over, the math speaks for itself.

---

Practical Observations:

Of course, this situation is purely hypothetical, and in practice, much depends on who buys shares on the exchange. Nonetheless, even if one group gains significant dominance, the situation could still be salvaged and reversed over many years because changes in this system progress more slowly. For every major investor in one group, there could always be an investor in the opposing group.

---

Final Remark:

The situation stabilizes almost automatically when there are more groups involved!

Conclusion:

So, even if we have two dominant factions and 3–4 or more groups whose members partially support one faction and partially the other, the process of one group gaining dominance over the other may never end in practice.

---

Opinion from ChatGPT:
Yes, you are right. In a scenario where two dominant factions exist and additional smaller groups (e.g., 3–4 or more) partially support both sides, the process of one faction gaining dominance over the other may indeed never conclude. There are several reasons for this:

---

1. Dynamic Balancing of Power

• Smaller groups constantly support the dominant factions, with support being diverse and variable (e.g., random or based on preferences).
• Even if one dominant faction gains an advantage in a given round, smaller groups can shift their support to the weaker faction in subsequent rounds. This creates a system of dynamic equilibrium, where differences in voting power between dominant factions remain relatively stable.

2. "Feedback" Mechanism in a Multi-Group System

• When one dominant faction begins to gain an advantage, smaller groups can naturally balance the system by choosing the weaker side to increase its chances. This can be driven by:
  • Sympathy for the underdog (e.g., the desire to support diversity).
  • Pragmatism (e.g., reducing the dominance of one group to limit the risk of a monopoly).
• Such a mechanism works similarly to an automatic stabilizer in an economic system.

3. Random Factors and Unpredictability of Support

• If the support of smaller groups is random (as in the simulation of random support flows), dominance by one group becomes even less likely. Even minimal changes in support allocation in one round can significantly influence the outcomes of subsequent rounds, causing the process of dominance to practically never reach a conclusion.

4. The Impact of Exponential Growth in Multi-Group Systems

• Exponential growth in dominance systems occurs when one group has a consistently larger share of support. In the case of multiple groups, the flow of support is more distributed, mitigating the rate of dominance escalation for one faction over another.

---

Numerical Example (2 Dominant Groups and 3 Smaller Groups):

• Group A (Dominant): 1.0 voting power.
• Group B (Dominant): 0.9 voting power.
• Groups C, D, E (Smaller): 0.7, 0.6, 0.5 voting power.
• In each round, smaller groups randomly allocate their support between A and B. Even with slight differences in support allocation, the voting power of dominant groups can remain in a state of relative equilibrium.

---

Mathematical Proof of Decentralization Without Downvotes:

From a mathematical standpoint, true decentralization of power is ONLY possible in a system without downvotes. Any forms of penalizing the other side radically tip the scales in favor of one group in a very short time, creating trends that are irreversible because the situation often unfolds too quickly to respond effectively.

Regards.