Hi there. In this math post, I showcase some quadratic equation word problems with a geometry theme. It is assumed that the reader is comfortable with solving quadratic equations, factoring methods, Pythagorean Theorem and the quadratic formula.
The amateurish math diagrams are screenshots taken while using the Math Is Fun Drawing tool.
Math text rendered in LaTeX with QuickLaTeX.com.

Example One - Advanced Rectangle Area
Consider the rectangle diagram below. The rectangle width is s + 1 units, the length is s + 3 units with a diagonal of 10 units. Find the area of the rectangle.
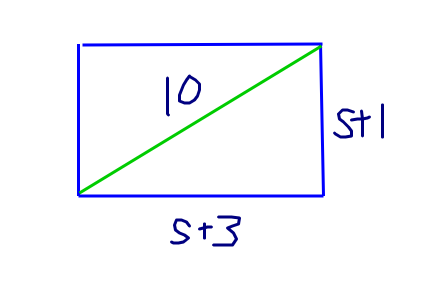
The area of the rectangle requires the length and width of the rectangle. Right now the variable s is an unknown value. This value for s can be solved for with the use of the Pythagorean Theorem/ Formula. We have the following:

It turns out that solving for the variable s is solving this Pythagorean quadratic equation.

Two numbers that multiply to negative 45 and add together to + 4 are +9 and -5. This leads into factoring the above as follows:

The two solutions for s are -9 and +5. Since the side length has to be non-negative (at least 0), the valid value for s is 5.
Referring back to the question, the rectangle width is 5 + 1 = 6 and the rectangle length is 5 + 3 = 8. This leads to the rectangle area of 48 square units.
Example Two - Circle Inside Circle
Refer to the diagram below. There is a small circle within a larger circle where they share to same middle point (origin). The small circle has a radius of 2 and the larger circle has a radius of 2 + x. Subtracting the small circle area from the larger circle's area results in 32 Pi square units. Determine the value of x.
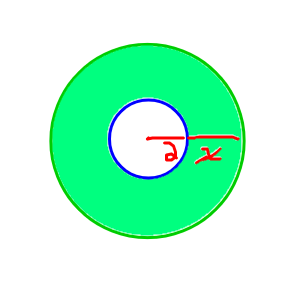
Larger Circle: 2 + x radius
Small Circle: 2 radius
Area Of Larger Circle - Area Of Small Circle = 32 Pi

Example Three - Garden With Surrounding Sidewalk
A 40 metre by 20 metre garden is surrounded by a sidewalk with a uniform width of x metres. The combined area of the garden and sidewalk is 1500 square metres. What is the sidewalk width?
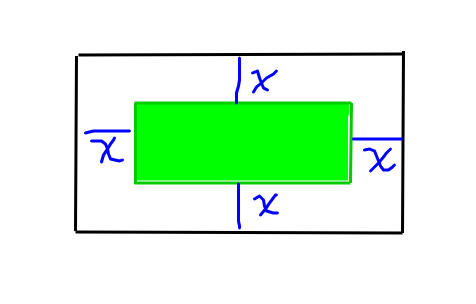

The length of the combined area is 40 metres + 2x metres as the sidewalk is on both sides of the middle garden. The width of the garden and sidewalk combined would be 20 + 2x metres.

Expanding the right side would reveal a quadratic equation.

Simplify and equate to zero for solving the quadratic.

Common factor out a four and complete the factoring.

The two solutions here are -35 and 5. As the sidewalk width cannot be negative, the valid solution is 5 metres.
