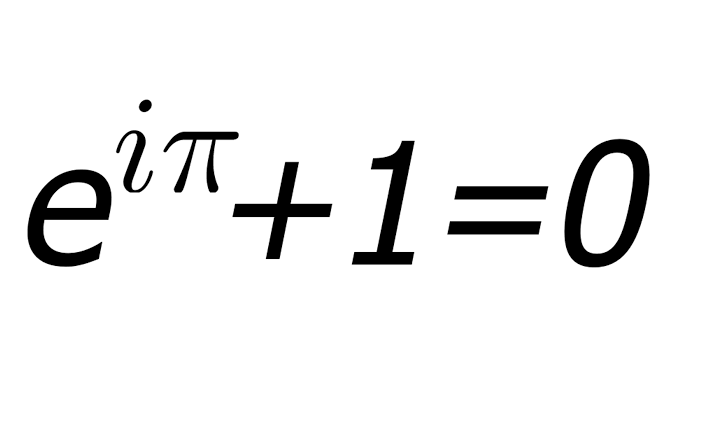
In my last post I focused on proving the existence of God by mathematics, particularly by Euler singularity formula. Euler singularity formula is
e^iπ+1=0
Where,
e= exponent. It is basically thr natural base of logarithm sector of mathematics. Here e includes logarithm in this singularity formula.
π= archimedes's constant. Which can be obtained by dividing the perimeter of a circle by its diameter. That means π include geometry in this Euler formula.
1= is multiplicative identity.
0= the presence of absence. 0 is discovered by an Indian mathematician named Aryabhata. He called 0 is the presence of absence.
All these four terms are real world entity in mathematics and is situated at real number set R.
i= unit of imaginary number. Which can be obtained by √(-1). This represent complex world entity to this singularity formula. And it is situated outside the range of real number. And there is no connection between real and complex number.
Now think that how can a imaginary entity be related to real world entity? Moreover the five terms used in this formula are from four different area. e from logarithm world, π from geometry, 1 and 0 from numerical world and i from complex world. How they can be related to each other if there is no super power?
You can define in other way too. e and π id irrational number which can't be ended by writing after decimal point. Which represent infinity but real world entity. On the other hand i is complex. That means e^iπ is combination of infinity, realiyy and imagination. Which has close relation to multiplicative identity one. Here 1 represent God as there is not more than one god. When we sum this reality, infinity, imagination and God we get zero, which is mainly the presence of absence. That means there must have God. 0 doesn't mean absolute absence. It is used to show something's absence which is present.
I hope you got it. If you have any question, ask me. And I will suggest you to think about it and acquire enough knowledge about e, i, π, 1, and 0. Then you can realize this properly. Thanks.