Exploring Image Compression using Singular Value Decomposition (SVD)

In this article, we delve into the application of Singular Value Decomposition (SVD) in image compression. The journey begins with an assignment from the CSE6040 Computing for Data Analysis course, focusing on linear algebra questions related to SVD. Drawing inspiration from the assignment, we embark on our personal capstone project to explore SVD and its implications in compressing images.
Introduction to SVD and Image Compression
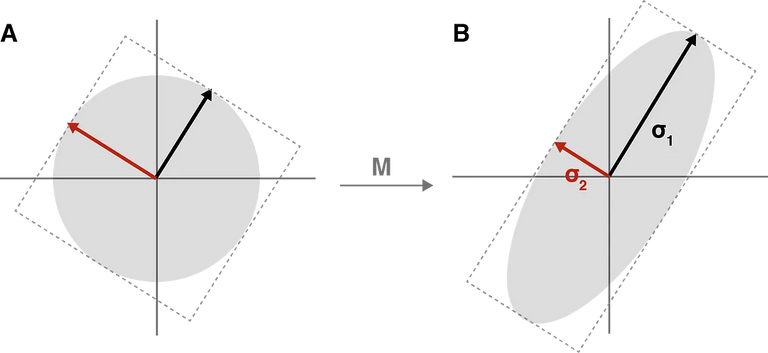
Singular Value Decomposition (SVD) is a powerful mathematical tool that decomposes a matrix into three component matrices: U, Sigma, and VT. Our focus lies on understanding how this decomposition aids in compressing images while retaining essential information.
Understanding Image Representation in Computing
Before delving into compression techniques, we examine how images are represented in a computing environment. Through code snippets and visualizations, we gain insights into the structure of image matrices and their properties.
Compression Techniques with SVD
We explore the intuition behind image compression using truncated SVD. By selecting a subset of singular vectors from each component matrix, we demonstrate how to approximate the original image with reduced dimensions.
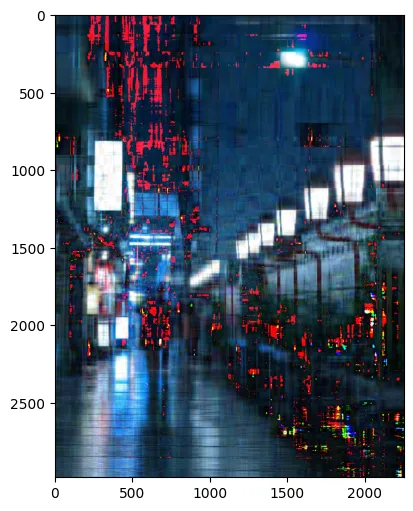
Practical Implementation: Greyscale Image Compression
Through code demonstrations, we compress a greyscale image using truncated SVD. We analyze the impact of selecting different numbers of singular vectors on image quality and storage efficiency.
Challenges and Solutions: Colour Image Compression
Extending our exploration to colour images, we encounter challenges unique to multi-channel data. We discuss heuristic approaches and objective methods for determining the optimal number of singular vectors.

Conclusion and Insights
Reflecting on our journey, we summarize key findings and insights:
Compression offers significant space savings while preserving image integrity.
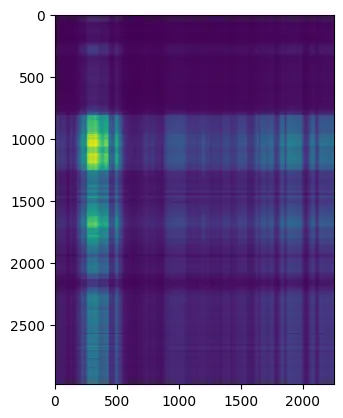
Objective methods aid in determining the optimal compression parameters.

Greyscale images are easier to compress compared to colour images, necessitating tailored approaches for each channel.
Through this project, we gain a deeper understanding of SVD's role in image compression and its practical implications in data analysis and visualization.
