The Fibonacci numbers are defined as the following sequence, with the current item is the sum of the previous two items.
F(1) = 0
F(2) = 1
F(N) = F(N - 1) + F(N - 2) for N >= 3
The first few Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21...
Of course, it is trivial to write a loop to sum the Fibonacci numbers of first N items.
function sumOfFib(n) {
let a = 0;
let b = 1;
let sum = 0;
for (let i = 1; i < n; ++ i) {
let c = a + b;
a = b;
b = c;
sum += a;
}
return sum;
}
Let's define the S function the sum of first few Fibonacci numbers:
S(1) = F(1) = 0
S(2) = F(1) + F(2) = 1
S(3) = F(1) + F(2) + F(3) = 2
S(4) = F(1) + F(2) + F(3) + F(4) = 4
S(5) = F(1) + F(2) + F(3) + F(4) + F(5) = 7
...
We notice that
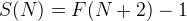
For example:
S(4) = F(6) - 1 = 5 - 1 = 4
S(3) = F(5) - 1 = 3 - 1 = 2
Using Induction to Prove the Fibonancci Sum Formula
S(1) = 0
S(2) = 1
Assume S(N) = F(N+2) - 1 stands.
S(N+1) = S(N) + F(N+1)
= F(N+2) + F(N+1) - 1
= F(N+3) - 1
And it also works for N+1!
Cancel Out the Fibonacci Numbers
We can rewrite the Fibonacci Formula as F(N) = F(N + 2) - F(N + 1).
Therefore,
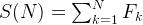
= F(2) - F(1) + F(3) - F(2) + F(4) - F(3) + .... F(N + 2) - F(N + 1)
Intermediate items are canceled out:
= F(N + 2) - F(1) = F(N + 2) - 1
How cool is that!
Reposted to Blog
Every little helps! I hope this helps!
Blurt On!~
If you like my work, please consider voting for me or Buy Me a Coffee, thanks!
https://steemit.com/~witnesses type in justyy and click VOTE

Alternatively, you could proxy to me if you are too lazy to vote!
Also: you can vote me at the tool I made: https://steemyy.com/witness-voting/?witness=justyy