[ESP/ENG] Imaginemos un Futuro con Cajeros de Criptomonedas y la Teoría de las Colas (1a parte). / Imagine a Future with Cryptocurrency ATMs and the Theory of Queues (Part 1).

Rad Bradbury, Julio Verne, Isaac Asimov y George Orwell entre otros han sido escritores que se han caracterizado por una visión futurista de sus temas. En ese momento y más tarde aún se lo llamó ciencia ficción.

Es decir, un argumento con un sustento científico pero que no ha sido probado aún ni lo será en el inmediato futuro.

Para los que hemos estudiado Estadística Económica sabemos que la Teoría de las Colas es un aspecto fundamental en los comportamientos de las personas en la actual sociedad moderna.

Es difícil pensar hoy en dia un aspecto de nuestras vidas en el que esta teoría no tenga su influencia.

Nacida en 1909 de la mano del matemático danés Agner Krarup Erlang para estudiar el redimensionamiento de las líneas y las centrales de los conmutadores telefónicos (él mismo era un empleado de la Copenhagen Telephone Exchange, subsidiaria de la Bell estadounidense) bien pronto se extendió con el correr de los años a muchos aspectos de la realidad económnica. Por ejemplo tiempos de espera en las cajas de los supermercados y en tiempos más modernos aún los tiempos de espera en ser servidos por un cajero automático bancario. Pasando por líneas de productividad en empresas (líneas de montaje), fechas de matriculación en las universidades, lavaderos de autos, restaurantes y casas de comidas, etc. La lista sería demasiado larga de enumerar.

La idea de este artículo es simular la llamada Teoría de las Colas en un cajero destinado a las criptomonedas (o al BTC para simplificar).

Los cajeros ya son una realidad en muchos países. Las colas, en un futuro no muy lejano, deberían ser una lógica consecuencia.

Para definir con exactitud el problema, en realidad se trata de definit con modelos matemáticos una determinada línea de espera y estableceder, de esa manera, una capacidad de servicio apropiada.

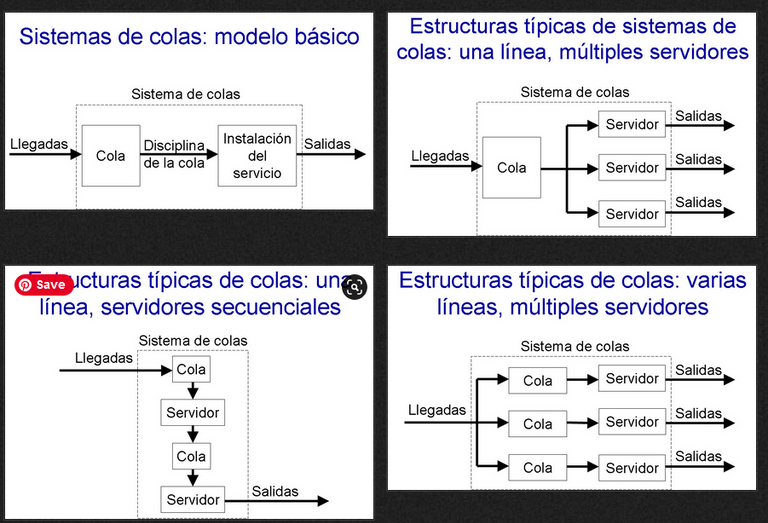
Para ello debemos analizar en primer lugar la estructura de la llamada "cola" y en particular los siguientes aspectos que la integran, ya que van a ser los elementos integrantes de los modelos matemáticos de los cuéles nos vamos a servir:
a) Las personas que integran esa cola: llamada básica que no es otra cosa que seleccionar una persona al azar (de todas las que van llegando e integrándose a la cola), servirle el servicio requerido, salir del sistema de colas y al final contabilizar el tiempo requerido desde su ingreso a la cola hasta su salida después del servicio efectuado exitosamente.

b) El tamaño y la capacidad de la cola: entendiendo por tal el número de potenciales clientes que pueden acudir a requerir el servicio. Y aqui se presenta un problema particular: que ese némero sea limitado (finito) o ilimitado (infinito).

Lo mismo vale para la capacidad de la misma, es decir, hasta cuantos usuarios o clientes es capaz de soportar.

c) El usuario o cliente entendido como unidad del modelo.

d) El mecanismo y la prioridad del servicio: esto se efectúa a través de fórmulas predefinidas que se suelen usar también en contabilidad y economía en general llamadas: FIFO (first in first out) que significa primero entrado primero servido; LIFO ( (last in first out) que el lo opuesta es decir el último que llega es el primero que se sirve; RSS (random selection of service) como su nombre lo expresa randomiza el servicio en modo aleatorio y Processor Sharing , un modelo moderno muy usado en la actualidad en la administración pública en donde todos los clientes son servidos de igual manera ya que existen varias colas simulténeas cuyos tiempos de espera fluyen de uno a otro. Es el clásica ejemplo de las Cajas de Jubilaciones donde los usuarios concurren a realizar distintos trámites y cada uno tiene una cola diversa de acuerdo al trámite que realiza.

Medio siglo más tarde, en 1953, otro matemático David G. Kendall introdujo una variante llamada A/B/C en la Teoría de las Colas, agregando precisamente algunas de las variables como la citada en el último párrafo, características de una economía en neta evolución y que estaban ausentes en el modelo original.

De esta manera se agregaron el número de los canales de servicio y, por ende, la capacidad del sistema para servir a todos esos canales, lo que traducido en otras palabras sería el número máximo de clientes permitidos: el tamaño de la población desde la cuál llegan los clientes y un orden de prioridad predefinido para servir los clientes en forma obligatoria: primero FIFO ahora traducido específicamente como First Come First Served (FCFS); después LIFO ahora llamado Last Come First Served (LCFS); luego el Random en esta ocasión bautizado como Service In Random Order (SIRO) y por último el Processor Sharing.

Hay que destacar que tanto FIFO como LIFO son términos estrictamente contables y por lo tanto el cambio de sigla obede més que nada a darle una connotación más cercana a la naturaleza del problema tratado.

Para desarrollar este modelo deberemos servirnos de:

a) La distribución de Poisson que es una distribución de probabilidad exponencial para analizar el comportamiento de los tiem pos de espera en la realización de un determinado evento.

b) El Modelo o Cadena de Markov que es una distribución de probabilidad que analiza las posibilidades de que la realización de un evento ocurra ocurra solamente dependiendo del evento inmediato anterior.

c) La notación de Kendall.

De cada uno de ellos me ocuparé en el próximo post.

Fuente/Source.

Rad Bradbury, Jules Verne, Isaac Asimov and George Orwell among others have been writers who have been characterized by a futuristic vision of their themes. At that time and later it was still called science fiction.

In other words, an argument with scientific support but that has not yet been proven and will not be in the immediate future.

For those of us who have studied Economic Statistics, we know that the Theory of Queues is a fundamental aspect in the behavior of people in today's modern society.

It is difficult today to think of an aspect of our lives in which this theory does not have its influence.

Born in 1909 by the hand of the Danish mathematician Agner Krarup Erlang to study the resizing of telephone lines and exchanges (he was himself an employee of the Copenhagen Telephone Exchange, a subsidiary of the American Bell), it soon spread with the over the years to many aspects of economic reality. For example, waiting times at supermarket checkouts and in more modern times even waiting times to be served by a bank ATM. Going through productivity lines in companies (assembly lines), enrollment dates in universities, car washes, restaurants and eating houses, etc. The list would be too long to list.

The idea of ​​this article is to simulate the so-called Theory of Queues in an ATM intended for cryptocurrencies (or BTC for simplicity).

ATMs are already a reality in many countries. Queues, in the not too distant future, should be a logical consequence.

To accurately define the problem, it is actually a matter of definitive with mathematical models a certain waiting line and establish, in this way, an appropriate service capacity.

To do this, we must first analyze the structure of the so-called "tail" and in particular the following aspects that make it up, since they will be the integral elements of the mathematical models of which we are going to serve:

a) The people who make up that queue: basic call that is nothing more than selecting a person at random (of all those who are arriving and joining the queue), serve the required service, exit the queue system and at the end count the time required from entering the queue to leaving after the successful service.

b) The size and capacity of the queue: understood as the number of potential customers who may come to request the service. And here a particular problem arises: that this number is limited (finite) or unlimited (infinite).

The same goes for its capacity, that is, up to how many users or clients it can support.

c) The user or customer understood as a unit of the model.

d) The mechanism and priority of the service: this is done through predefined formulas that are usually used also in accounting and economics in general called: FIFO (first in first out) which means first in first served; LIFO ((last in first out) that the opposite is to say the last one that arrives is the first one that is served; RSS (random selection of service) as its name expresses it randomizes the service in random mode and Processor Sharing, a modern model Currently widely used in public administration where all clients are served in the same way since there are several simultaneous queues whose waiting times flow from one to another.

It is the classic example of Retirement Savings Banks where users concur to perform different procedures and each one has a different queue according to the procedure it carries out.

Half a century later, in 1953, another mathematician David G. Kendall introduced a variant called A / B / C in the Queuing Theory, adding precisely some of the variables such as the one cited in the last paragraph, characteristics of a net economy. evolution and that were absent in the original model.

In this way, the number of service channels and, therefore, the capacity of the system to serve all those channels were added, which translated in other words would be the maximum number of clients allowed: the size of the population from which customers arrive and a predefined order of priority to serve customers on a mandatory basis: first FIFO now specifically translated as First Come First Served (FCFS); later LIFO now called Last Come First Served (LCFS); then the Random on this occasion baptized as Service In Random Order (SIRO) and finally the Processor Sharing.

It should be noted that both FIFO and LIFO are strictly accounting terms and therefore the acronym change obeys more than anything to give it a connotation closer to the nature of the problem dealt with.

In order to develop this model we will have to use:

(a) The Poisson distribution which is an exponential probability distribution to analyze the behavior of the waiting times in the realization of a certain event.

b) The Markov Model or Chain, which is a probability distribution that analyzes the possibilities of the occurrence of an event occurring only depending on the immediately preceding event.

c) Kendall's notation.

I will deal with each of them in the next post.

Fuente/Source.

Bibliografia consultada / Consulted bibliography:

• Henk Tijms: Algorithmic Analysis of Queues, Capítulo 9 en A First Course in Stochastic Models, Wiley, Chichester, 2003
• Distribución de Poisson.
• Ejemplo de una Cadena de Markov.
• Elementos de la Teoría de las Colas
• La Notación de Kendall.

Fuente de la imagen que ilustra el inicio de este post: Claudio Schwarz modificada por el autor. / Source of the image that illustrates the beginning of this post: Claudio Schwarz modified by the author.

Blogs, Sitios Web y Redes Sociales / Blogs, Webs & Social Networks	Plataformas de Contenidos/ Contents Platforms
Mi Blog / My Blog	Los Apuntes de Tux
Mi Blog / My Blog	El Mundo de Ubuntu
Mi Blog / My Blog	Nel Regno di Linux
Mi Blog / My Blog	Linuxlandit & The Conqueror Worm
Mi Blog / My Blog	Pianeta Ubuntu
Mi Blog / My Blog	Re Ubuntu
Mi Blog / My Blog	Nel Regno di Ubuntu
Red Social Twitter / Twitter Social Network	@hugorep

Blurt Official	Blurt.one	BeBlurt	Blurt Buzz